Modified three stick triangle problem

Studying at PUC-Rio there was a course called Probabilistic Models given by the Telecommunication Engineering Department, which was well-known for their creative approach to student evaluation. In one of those exams there was a question described below:

Suppose you break a stick in a random point of its length, from the two pieces you have now, choose the largest piece and break again randomly. What is the likelihood of you form a triangle with the three pieces?

Before you go nuts looking in Google, note that this problem is slightly different from the "three stick triangle problem" , in ours the second time you choose to break the biggest piece which is different of breaking a stick into 3 pieces directly. Warning: if you want to try to solve it, stop reading now. There are two ways to solve this problem, a computational way, that was not the case at the time, and an analytical form. The analytic form is interesting but requires further mathematical knowledge. But a computational form is available for anyone who knows how to program as in the Python script below.

from  random  import  random
def isTriangle ( a , b , c ) :
        listT =  [ a , b , c ] 
        listT. sort ( ) 
        if  ( listT[2] < (listT[1] + listT[0])) :
                 return True 
        else :
                 return False
 
def breakRule ( ) :
        p =  random ( ) 
        if  ( p <  0.5 ) :
                a = p
                p1 =  random ( ) 
                b =  ( 1 -p ) * p1
                c =  ( 1 -p ) - b
         else :
                a =  ( 1.0 - p ) 
                p1 =  random ( ) 
                b = p * p1
                c = p - b
         return isTriangle ( a , b , c )
 
yes =  0 
no =  0
 
for i in  xrange ( 100000 ) :
         if breakRule ( ) :
                yes + =  1 
        else :
                not + =  1
 
print  "Number of times that worked:% d" % yes
print  "Number of times that went wrong:% d" % not
print  "Probability:% f" % ( float (yes)) / (yes + no)

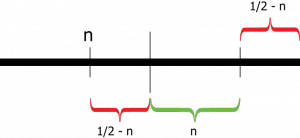
Now let's see how to solve it analytically. <continue> Considering the ruler as having length 1, we divide the problem into two parts that are symmetrical. In the first part the break occurred at the point n ( 0 <n <0.5 ) until 50% of the length of the ruler. Thus the second break may not occur, to respect the triangular inequality:

$latex A>B+C$

where A is the length of the longest piece in the sections:

$latex [N,\frac{1}{2}];[1-(\frac{1}{2}-n);1]$

As you can see in the figure below: